Soal Rata Rata dengan Pertidaksamaan

Dari buku GRE Quantitative Reasoning. Perhitungan di atas kurang mewakili persamaan. Karena di dalamnya ada kata kata more than twice, berarti tidak bisa direpresentasikan denan simbol sama dengan. Pasti angkanya akan lebih dari 2 sehingga hasil bagi akan lebih kecil, bukan sama dengan (ingat, lebih besar dari sebauh kuantitas yang diletakan dibawah sebagai pembagi akan menghasilkan nilai yang lebih kecil. Sehingga hasil akan lebih kecil.

Soal Aljabar SD dengan Solusi Brute Force

Ada banyak metoda yang dapat dipakai dalam menyelesaikan soal aljabar. Salah satunya adlaah Brute force. cara ini cocok untuk anak SD yang belum banyak berlatih dan mengenal solusi aljabar cara distribusi atau eliminasi.

Ada angka dua digit yang nilainya kurang dari 80. Angka ini besarnya 58
lebih banyak dari hasil kali kedua digitnya. Temukan angka tersebut.

Misal, angka  dibaca: ab = 10a + b, di mana 10a + b < 80.

Mari kita membuat persamaan:
10a + b = (axb) + 58.
Dari persamaan ini kita bisa menebak kalau angka 10a + b akan lebih besar dari 58, tidak mungkin lebih kecil. Maka a>5.

Membuat persamaan dari sini agak sulit akrena tidak ditentukan dnegan pasti nilai maksimum dari angka ab, hanya ditulis ab kurang dari 80 (berarti bisa 79, 78 dst). 

Jadi cara yang lebih mudah untuk anak anak adalah dengan mencoba satu per satu (Brute Force). 

Carilah angka 2 digit yang kalau digitnya dikali dan ditambah 58, hasilnya akan sama dengan angka itu sendiri. tgernyata begitu kalimat lain dari soal tersebut. Angka 2 digit itu juga harus kurang dari 80.

Jawaban: 72.

Adakah yang dapat menemukan jawaban dengan cara lain? 

Soal dari Matematika kelas 5, Pengarang : Peterson Hal 52 no 197. 

Bereksperimen dengan pylab

Menginstall pylab

bash$ python3 -m pip install matplotlib

Membuat grafik di pylab

import pylab

pylab.figure(1)

pylab.plot([1,2,3,4], [1,7,3,5])

pylab.show() 

-------------------------------------------

Menghitung bunga menggunakan pylab

import pylab

principal = 10000

interestRate = 0.1

years = 20

values = []

for i in range(years + 1):

    values.append(principal)

    principal += principal*interestRate

pylab.plot(values)

pylab.show()

--------------------------------------------------

Mengubah style di pylab

import pylab

principal = 10000

interestRate = 0.1

years = 20

values = []

for i in range(years + 1):

    values.append(principal)

    principal += principal*interestRate

pylab.title("5% Growth, Compounded Annually", fontsize = "xx-large")

pylab.xlabel('Years of Compounding')

pylab.ylabel('Value of Principal ($)')

pylab.plot(values, linewidth = 30)

pylab.plot(values)

pylab.show()

------------------------------------------

Kesetimbangan Kimia (Kimia SMA Kelas 11)

Jenis reaksi

Ada reaksi yang dapat berlangsung satu arah ada yang dua arah.  

Reaksi dinitrogen  tetroksida dan nitrogen dioksida adalah salah satu reaksi yang dapat terjadi 2 arah. 

Yang terjadi ketika reaksi:

 

Ketika N2O4 belum banyak yang terurai,  campuran masih tidak berwarna yang menunjukkan jumlah NO2 yang dihasilkan masih sedikit.  Reaksi akan terus berlangsung dan akan semakin banyak NO2 yang dihasilkan sampai menuju kesetimbangn. Pada saat ini konsentrasi NO2 dan N2O3 tidak berubah dan reaksi berlangsung 2 arah.

Ketika sistem mencapai kesetimbagan  maka konstanta laju reaksi sebelum dan sesudah reaksi sama. (Kfwd dan Krev). Perbandingan konstanta laju reaksi  juga sebanding dengan perbandingan konsentarasi tiap senyawa dengan pangkat koefisiennya

Perbandingan di atas disebut konstanta keseimbangan (K). K menunjukkan seberapa banyak rekasi menghasilkan produk. Nilai k berbeda beda.

Nilai  K yang kecil menunjukkan reaksi belum berlangsung dengan sempurna, K besar berarti hampir seimbang dan K yang sama berarti rekasi dalam kesetimbangan .

Hasil bagi reaksi (Q)

Hasil bagi reaksi berhubungan dengan jumlah produk dan reaktan dalam reaksi kimia pada suatu titik waktu tertentu. Jika hasil reaksi dapat dibandingkan dengan K untuk memprediksi arah reaksi kimia terhadap kesetimbangan. 

Contohnya pada reaksi: 

 

Maka hubungan Q dan K seperti pada gambar: 

Jika terdapat reaksi: 

 

Perbandingan Qc dan Kc

• Q_c = K_c , reaksi telah mencapai kesetimbangan. Jika Q_c = K_c, reaktan ⇌ produk
• Q_c < K_c , reaksi akan berlangsung dari arah kiri ke kanan (pembentukan produk) hingga mencapai kesetimbangan kimia (Q_c = K_c). Jika Q_c < K_c, reaktan → produk
• Q_c > K_c , reaksi akan berlangsung dari arah kanan ke kiri (pembentukan reaktan) hingga mencapai kesetimbangan kimia (Q_c = K_c). Jika Q_c > K_c, reaktan ← produk

Perhitungan yang melibatkan Q dan K, ringkasnya :

Selain Kc, ada juga konsentrasi kesetimbagang berdasar tekanan (Kp). Hubungan Konstanta kesetimbangan berdasar konsentrasi (Kc) dan Konstanta kesetimbangan berdasar Tekanan (Kp)

 

Perhitungan hasil bagi     reaksi gas NO2 menjadi NO dan O2:

Asas Le Chatelier

Adalah asas kesetimbangan yang terjadi dalam reaksi kesetimbangan seperti di bawah ini: 

 Contohnya:

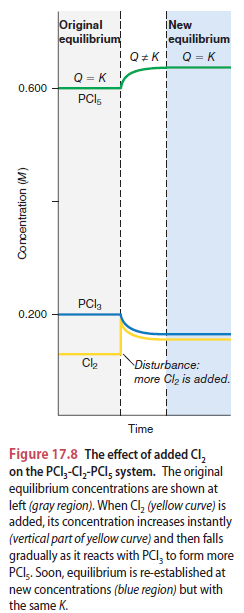
Pada grafik: 

 Visualisasi perubahan tekanan dan volume:

 

Perubahan temperatur

 Reaksi ke arah PCl5 mengeluarkan kalor (Hrxn negatif- reaksi eksoterm)

Perubahan Konsentrasi, tekanan atau Volume, perubahan suhu, dan Pengaruh Katalis secara ringkas  dapat dilihat pada tabel ini:

 

Van

Hoff Equation- Perubahan T dan hubungannya dengan K: 

Untuk reaksi endoterm, penambahan temperatur akan menyebabkan reaksi bergeser ke kanan dan K akan bertambah. Untuk reaksi eksoterm terjadi sebaliknya.

Sumber materi:

• https://www.studiobelajar.com/kesetimbangan-kimia/
• https://kimia2018.wordpress.com/kimia-kelas-xi/semester-i/bab-4-kesetimbangan/

 Latihan soal:

• https://tanya-tanya.com/contoh-soal-dan-pembahasan-reaksi-kesetimbangan/
  

 

 

Merakit Train Seesaw Dengan Lego Technic 9686

Dulu, kami sering membuat mainan bergerak dari barang bekas. Tapi ternyata mainan seperti ini walaupun senang memainkannya, agak sulit dibuat dan tidak tahan lama. Apalagi ada bagian bagin yang memang membutuhkan ukuran dan presisi yang cukup besar seperti roda gigi, katrol, roda, dan lain lain. cara paling mudah untuk membuat mainan ini memang cari lagi bagian yang kurang bisa dibuat dari kertas dan kardus. cara lain paling sederhana adalah menggunakan Lego. Lego technic 9686 terdiri dari banyak bagian yang mengasyikkan seperti berbagai macam roda gigi, batang berlubang, poros, berbagai macam sekrup, dan lain lain. 

Lego technic ini dilengkapi dengan beberapa contoh mesin sederhana untuk anak anak SMP dan SD. Ada juga lembar eksperimen sains jika anak suka mencoba. namun merakit dan memainkannya sudah dapat memberi manfaat utnuk anak. 

Setelah semua mesin sederhana selesai dirakit, timbul lagi keinginan untuk merancang sendiri mesin atau mainan sederhana. Kebetulan di Youtube masih jarang contoh mainan sederhana yang dibuat dari Lego technic.

 Ini adalah Train Seesaw, yang awalnya adalah mainan kereta api dalam rel yang dapat melewati jembatan jungkat jungkit. Mainan ini dapat ditemukan di:

• https://www.thingiverse.com/thing:65965
  
• https://www.instructables.com/Train-Seesaw/ 

https://www.instructables.com/Train-Seesaw/

Mainan ini dapat juga dibuat dari Lego Technic 9686. Di bawah ini adalah video cara membuatnya.

 

 

Dynamic Programming di Python

Ini adalah salah satu materi yang ada di buku Pemrograman Kompetitif. Buku ini bisa di download di https://tlx.toki.id/courses/competitive/chapters/07/lessons/A. Seharusnya penjelasannya diketik ulang , tapi maaf belum sempat... 

Dalam buku dijelaskan konsep dan Pseudocode dari soal. Keduanya diterjemahkan dalam bahasa Python versi saya.

Soalnya seperti ini:

Diberikan M jenis koin, masing-masing jenis bernilai a₁,a₂, ....aₘ rupiah. Asumsikan banyaknya koin  yang ada tak terbatas. Tentukan banyaknya koin paling sedikit untuk membayar tepat sebesar N rupiah!

Solusinya bisa diselesaikan dalam dua cara: Bottom up dan Top down.

1. Bottom-up: (ubah variabel M dan N untuk mengubah input)

1. def solve(a, N):
2.     f = [0] * (N + 1)
3.     for x in range(1, N + 1):
4.         best = float('inf')
5.         for k in range(len(a)):
6.             if a[k] <= x:
7.                 best = min(best, f[x - a[k]] + 1)
8.         f[x] = best
9.     return f[-1]
10. 
    
11. def main():
12.     M = 1, 6, 10
13.     N = 12
14.     print(solve(M, N))
15. 
    
16. if __name__ == '__main__':
17.     main()

2. Top-down:

1. def solve(x):
2.     if x == 0: return 0
3. 
   
4.     best = float('inf')
5.     for k in range(len(M)):
6.         if M[k] <= x:
7.             best = min(best, solve(x - M[k]) + 1)
8.     return best
9. 
   
10. def main():
11.     global M
12.     M = 1000, 2000, 5000
13.     N = 12000
14.     print(solve(N))
15. 
    
16. if __name__ == '__main__':
17.     main()